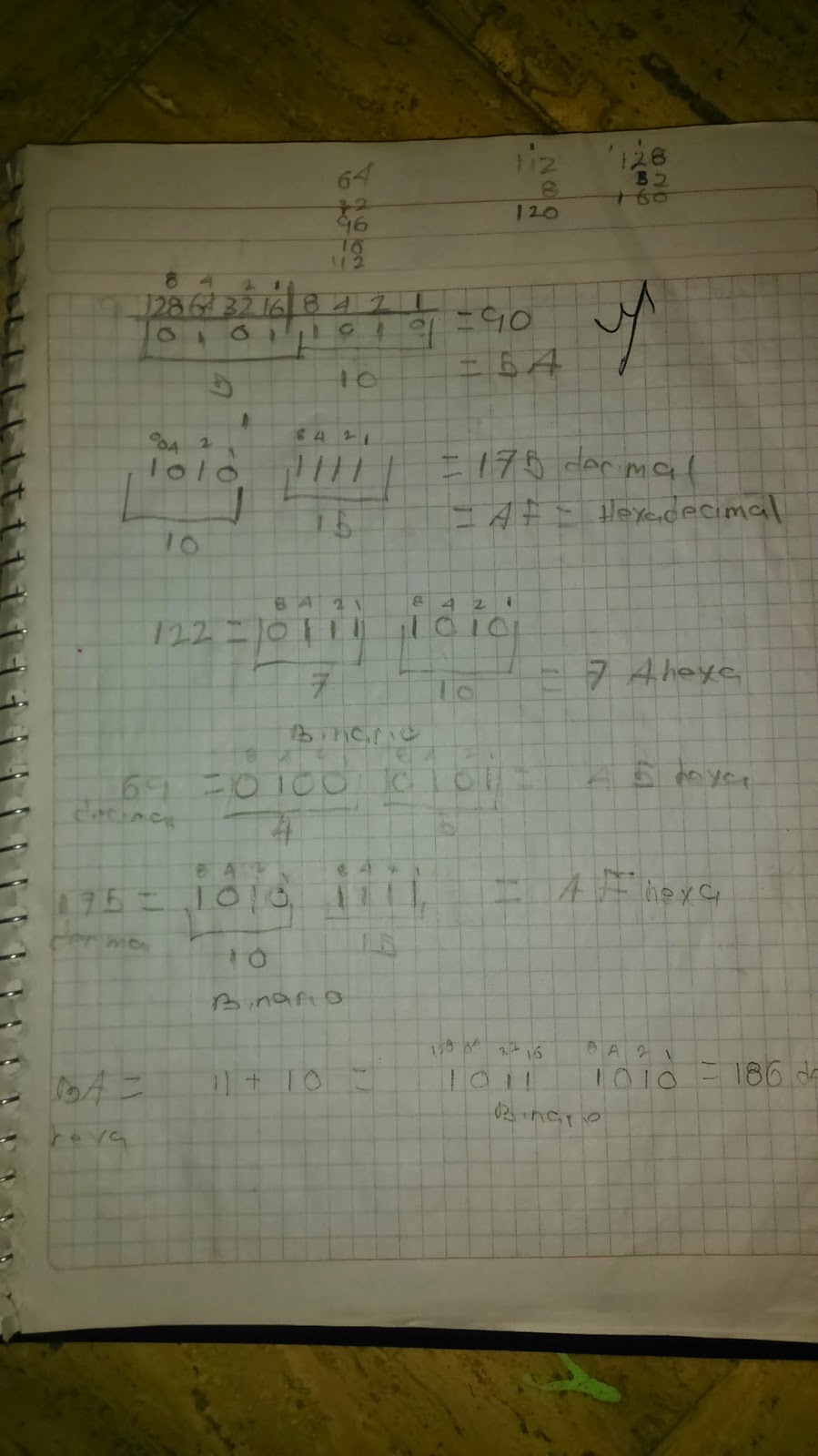13 de enero del 215
Números romanos
Este sistema (tan bien conocido por nosotros) tuvo el mérito de ser capaz de expresar los números del 1 al 1.000.000 con sólo siete símbolos: I para el 1, V para el 5, X para el 10, L para el 50, C para el 100, D para el 500 y M para el 1.000. Es importante acotar que una pequeña línea sobre el número multiplica su valor por mil.
En la actualidad los números romanos se usan para la historia y con fines decorativos. La numeración romana tiene el inconveniente de no ser práctica para realizar cálculos escritos con rapidez.
Prácticamente todo el mundo occidental conoce los números romanos. Se enseñan en las escuelas, se pueden ver en créditos de muchas películas, marcan los siglos y se usan para distinguir reyes del mismo nombre.
Los números romanos también se pueden encontrar con mucha frecuencia en los relojes. Sin embargo, a veces vemos una pequeña peculiaridad. Por lo general se enseña que el número 4 debe ser escrito IV, pero en muchos relojes este número está representado como IIII. ¿De dónde surge esta notación?
El sistema numérico de los romanos fue derivado, según investigaciones arqueológicas, del utilizado por los etruscos, una civilización que habitó Italia entre los siglos VII y IV antes de Cristo. Los romanos utilizaron este sistema, que se basaba en el método aditivo. I y I eran II, V y II eran VII, y II y II eran IIII. El número para 40 era XXXX y el nueve era representado como VIIII. Con el tiempo, los romanos empezaron a utilizar el método sustractivo, en el que un número anterior resta su cantidad a la siguiente. Así, en lugar de escribir 9 como la suma de 5 y 4 (VIIII) se escribió como la resta de 10 menos 1 (IX). La ventaja de este método era que acortaba la notación de los números, pues se usaban menos símbolos. De esta forma el número IIII pasó a ser IV.
El sistema sustractivo fue utilizado en los tiempos del Imperio Romano. Pero si se había hecho esta reforma, ¿por qué se utilizó la notación del IIII en vez del IV en los relojes medievales? De hecho, el 4 es el único número que se representa de esta forma, pues el nueve es representado como IX, y no como VIIII.
Entre las razones por las que se aduce que el sistema aditivo está el de la confusión que se puede producir entre el número IV y el número III, ambos escritos con tres trazos. La confusión se acentúa al estar ambos inclinados por su posición en el círculo de la cara del reloj. Al escribirse como IIII se marcaba mejor la diferencia.
Otra explicación dice que al escribirse el 4 de este modo le daba simetría al estar frente al número 8 (VIII) que se encuentra al otro lado del reloj. El V no balancea al VII pues no tienen notaciones alternativas. El X y el II tienen ambos trazos y en el caso del IX lo forman tres líneas al igual que el III.
1=I 2=II 3=III 4=IV 5=V 6=VI 7=VII 8=VIII 9=IX 10=X 50=L 100=C 500=D 1000=M
http://www.profesorenlinea.cl/universalhistoria/Roma/RomaNumerosHistoria.htm
ejercicios realizados en clase
convertir los siguientes números arábigos a romanos
100, 224, 18, 544, 894, 975, 1022, 496, 786, 849, 2952, 1365, 3798, 2999
Números arábigos
Los números arábigos, también llamados números indoarábigos son los símbolos más utilizados para representarnúmeros. Se les llama "arábigos" porque los árabes los introdujeron en Europa aunque, en realidad, su invención surgió en la India. El mundo le debe a la cultura india el invento trascendental del sistema de numeración posicional, así como el descubrimiento del 0, llamado śūnya (shuunia) o bindu en lengua sánscrita, aunque los mayas también conocieron el 0. Los matemáticos persas de la India adoptaron el sistema, de quienes lo tomaron los árabes. Para el momento en que se empezaron a usar en el norte de África, ya tenían su forma actual, de allí fueron adoptados en Europa en la Edad Media. Su uso aumentó en todo el mundo debido a la colonización y comercio europeos.
El sistema "arábigo" se ha representado (y se representa) utilizando muchos conjuntos de glifos diferentes. Estos glifos pueden dividirse en dos grandes familias, los numerales arábigos occidentales y los orientales. Los orientales, que se desarrollaron en lo que actualmente se corresponde a Irak, se representan en la tabla que viene a continuación como Arábigo-Índico. El Arábigo-Índico oriental es una variedad de los glifos arábigo-índicos. Los numerales arábigos occidentales, desarrollados en Al-Ándalus y elMagreb se muestran en la tabla como Europeo
En Japón, los números "arábigos" y el alfabeto latino forman parte del sistema de escritura rōmaji. Así, si un número está escrito con glifos "arábigos", en Japón dirán que “está escrito en rōmaji” en contraposición a la numeración japonesa.
Historia
El sistema de numeración arábigo se considera uno de los avances más significativos de las matemáticas. La mayoría de los historiadores coinciden en afirmar que tuvo su origen en la India (los árabes se refieren a este sistema de numeración como “Números Indios”, أرقام هندية, arqam hindiyyah), y se expandió por el mundo islámico y de ahí, vía al-Andalus, al resto de Europa.
Se especula que el origen del sistema posicional base 10 utilizado en la India tuviera sus orígenes en China. El sistema chino Hua Ma (ver Numeración china) es también posicional y de base 10 y pudo haber servido de inspiración para el sistema que surgió en la India. Esta hipótesis cobra fuerza por el hecho de que entre los siglos V y VIII (periodo durante el cual se desarrolló el sistema numérico indio) coincidió con una gran afluencia de peregrinos budistas entre China y la India. Lo que es cierto es que en la época de Bhaskara I (Siglo VII) en la India se utilizaba un sistema numeral posicional base 10 con 9 glifos, y se conocía el concepto delcero, representado por un punto.
Este sistema de numeración llegó a Oriente Medio hacia el año 670. Matemáticos musulmanes del actual Irak, como al-Jwarizmi, ya estaban familiarizados con lanumeración babilónica, que utilizaba el cero entre dígitos distintos de cero (aunque no tras dígitos distintos de cero), así que el nuevo sistema no tuvo un buen recibimiento. En el siglo X los matemáticos árabes incluyeron en su sistema de numeración las fracciones. al-Jwarizmi escribió el libro "Acerca de los cálculos con los números de la India" cerca de el año 825 y Al-Kindi escribió "El uso de los números de la India" en cuatro volúmenes. Su trabajo fue muy importante en la difusión del sistema de la India en el Oriente Medio y en el occidente.1
Las primeras menciones de estos numerales en la literatura occidental se encuentran en el Codex Vigilanus del año 976.2 A partir de 980 Gerberto de Aurillac (más tarde papa con el nombre de Silvestre II, hizo uso de su oficio papal para difundir el conocimiento del sistema en Europa. Fibonacci, un matemático italiano que había estudiado en Bugía (en la actual Argelia), contribuyó a la difusión por Europa del sistema arábigo con su libro Liber Abaci, publicado en 1202. Entre los primeros países se hallaba Gran Bretaña, teniéndose escritos como una en lino de la iglesia de Braye de 1448 en Berkshire y una en Escocia de 1470 en la tumba de Eral de Huntly, en.3 En Europa central, el rey de Hungría Ladislao el Póstumo, comenzó a utilizar los números arabigos, teniéndose registro de un documento real de 1456.4
Sin embargo, no fue sino hasta la invención de la imprenta en 1450, cuando este sistema de numeración comenzó a utilizarse de forma generalizada en Europa; para el siglo XV son ya utilizados ampliamente; por su parte, los números arábigos reemplazaron a la numeración cirílica en Rusia alrededor de 1700, cuando fueron introducidos por el zar Pedro I de Rusia.
http://es.wikipedia.org/wiki/N%C3%BAmeros_ar%C3%A1bigos
centena-decena-unidad . decimas centecimas milecimas
ejercicios realizados en clase
realiza la siguiente suma de números arábigos
0.8+0.3 1.8+2.3 6.40+0.58 7.31+1.53 0.062+0.710 0.153+2.820 3.418+12.790 22+05 1000+550
sistema binario
El sistema binario, o sistema en base 2, emplea sólo dos dígitos (el 0 y el 1).
La importancia del sistema binario estriba en la facilidad para codificar los dos símbolos distintos que emplea, el 0 y el 1, a nivel eléctrico o electrónico, mediantecontactos abiertos o cerrados (no pasan/pasan electrones) o como ausencia/presencia de tensión eléctrica.
Cuando el valor binario es 0 el contacto se abre (no pasan electrones), se dice pues que tiene un estado bajo, negado o falso.
Cuando el valor bianrio es 1 el contacto se cierra (pasn electrones), se dice pues que tiene un estado alto, no negado o verdadero.
En el interior de los ordenadores, en los procesadores y en los dispositivos de almacenamiento, se aprovecha la codificación electrónica del sistema binario y se maneja o almacena exclusivamente información en formato digital; por sus circuitos circulan o no ciculan electrones. Cada dígito del sistema binario así codificado se denomina bit.
Existen otros sistemas de numeración, como el hexadecimal y el octal, que se emplean en computación.
El sistema hexadecimal, o sistema en base 16, emplea 16 dígitos y como los árabes representan los números, sólo son 10, se añaden las letras A, B, C, D, E y F. Su utilización está muy vinculada con la informática ya que 16 es una potencia exacta de 2.
El sistema de numeración octal, o sistema de base 8, emplea ocho dígitos (entre 0 y 7). Como en el caso del sistema hexadecimal, la base de numeración del sistema octal es una potenci aexacta de 2, razón por la que también es empleado en informática.
http://colegiolacolina.creatuforo.com/introduccin-al-sistema-binario-tema360.html
Código binario, decimal y hexadecimal
|
De decimal a binario
Para hacer la conversión de decimal a binario, hay que ir dividiendo el número decimal entre dos y anotar en una columna a la derecha el resto (un 0 si el resultado de la división es par y un 1 si es impar).
La lista de ceros y unos leídos de abajo a arriba es el resultado.
Ejemplo: vamos a pasar a binario 7910
79 1 (impar). Dividimos entre dos:
39 1 (impar). Dividimos entre dos:
19 1 (impar). Dividimos entre dos:
9 1 (impar). Dividimos entre dos:
4 0 (par). Dividimos entre dos:
2 0 (par). Dividimos entre dos:
1 1 (impar).Por tanto, 7910 = 10011112
http://recursostic.educacion.es/secundaria/edad/4esotecnologia/quincena5/4q2_contenidos_2c.htm
ejercicios realizados en clase
convertir los siguientes números decimales a binarios
198, 80, 150, 222, 51 |
Procedimiento:
- Dividir entre 2 sucesivamente
- Apuntar el resultado y el resto de cada operación
- Apuntar a lista de ceros y unos de abajo a arriba
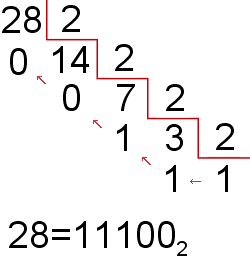 |
|
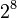 valores posibles, y esto puede representarse como
valores posibles, y esto puede representarse como 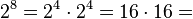
 , que equivale al número en base 16
, que equivale al número en base 16 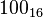 , dos dígitos hexadecimales corresponden exactamente a un byte.
, dos dígitos hexadecimales corresponden exactamente a un byte.