Sistema hexadecimal
El sistema hexadecimal (a veces abreviado como Hex, no confundir con sistema sexagesimal) es el sistema de numeración posicional que tiene como base el 16. Su uso actual está muy vinculado a la informática y ciencias de la computación, pues los computadores suelen utilizar el byte u octeto como unidad básica de memoria; y, debido a que un byte representa 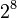 valores posibles, y esto puede representarse como
valores posibles, y esto puede representarse como 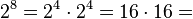
 , que equivale al número en base 16
, que equivale al número en base 16 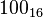 , dos dígitos hexadecimales corresponden exactamente a un byte.
, dos dígitos hexadecimales corresponden exactamente a un byte.
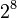 valores posibles, y esto puede representarse como
valores posibles, y esto puede representarse como 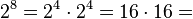
 , que equivale al número en base 16
, que equivale al número en base 16 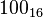 , dos dígitos hexadecimales corresponden exactamente a un byte.
, dos dígitos hexadecimales corresponden exactamente a un byte.
En principio, dado que el sistema usual de numeración es de base decimal y, por ello, sólo se dispone de diez dígitos, se adoptó la convención de usar las seis primeras letras del alfabeto latino para suplir los dígitos que nos faltan. El conjunto de símbolos sería, por tanto, el siguiente:
Se debe notar que A = 10, B = 11, C = 12, D = 13, E = 14 y F = 15. En ocasiones se emplean letras minúsculas en lugar de mayúsculas. Como en cualquier sistema de numeración posicional, el valor numérico de cada dígito es alterado dependiendo de su posición en la cadena de dígitos, quedando multiplicado por una cierta potencia de la base del sistema, que en este caso es 16. Por ejemplo: 3E0A16 = 3×163 + E×162 + 0×161 + A×160 = 3×4096 + 14×256 + 0×16 + 10×1 = 15882.
El sistema hexadecimal actual fue introducido en el ámbito de la computación por primera vez por IBM en 1963. Una representación anterior, con 0–9 y u–z, fue usada en 1956 por la computadora Bendix G-15.
http://es.wikipedia.org/wiki/Sistema_hexadecimal
convercion de decimal a hexadecimal
de hexadecimal a decimal 
primero el numero hexadecimal se convierte a binario
ejemplo: FA= F=15 A=10 pasar el 15 y el 10 a binario tomando la solo en cuenta del 1 al 8
15= 1111 10=1010 después se junta el 15 y el 10 binario
=11111010 esto se pasa a decimal =250 decimal



No hay comentarios:
Publicar un comentario